Trees

A tree imposes a hierarchical structure on a collection of items. Trees are structurally a lot like linked lists i.e it is a collection of elements called nodes. Actually, a linked list is a simplistic kind of tree. Recall that a linked list “node” had a value and a “next” pointer. The tree structure also has (one or more) values plus (one or more) pointers:

class Tree {
public:
    double value;
    Tree *left, *right;
};

The only difference with a linked list is that the tree has two “next pointers,” or as we label them in the class, a “left” and “right” next pointer.

Unlike the linked list, we use the NULL (bogus) pointer to indicate that either the left or right pointers point to nothing. In the linked list, we didn’t worry about NULL because we had another variable, count, that told us how many values were in the list. This will not work with trees, because trees are not linear.

A tree can have any number of next pointers; if it always has two (each of which may or may not equal NULL), like we will do here, it’s a binary tree. Surely you imagine a tree that had three pointers, or even an array or vector of pointers, rather than just two.

Thus, a tree’s “next pointers” are more like “children” — each node in a binary tree has zero, one, or two children. Those children are also trees. Additionally, a tree has only one “parent.” That is to say, for each node in the tree, either that node is the top (the “root”) or only one node links to it (it is the child of only one node).

If we did not restrict trees in this way, and allowed different nodes to link to the same children, then our algorithms for processing such structures would become more complicated. Actually, we wouldn’t even call them trees anymore; the correct terminology is “graph.” A graph is a structure where every node can have links to any other node, even back to itself (so trees are a kind of graph).

We will actually be creating graphs in later Homeworks, but for now we will concern ourselves only with trees.

Building a tree

The rest of these lecture notes will refer specifically to Homework 5 requirements.

In Homework 5, each tree node contains two values (besides the pointers): a string op value and a double val value. The idea is that the op will equal "" when the node has a numeric value (stored in val), and op will not equal "" when the node represents a mathematical operation (in such cases, op may equal "+" or "log", for example).

Thus, here is our new tree structure:

class Tree
{
public:
    std::string op;
    double val;
    Tree *left;
    Tree *right;
};

(We use std::string instead of string in case using namespace std; has not been activated.)

Let’s now build a tree. Suppose we want to represent the expression 3.4-(2.6+5.0). This is what the tree should look like:

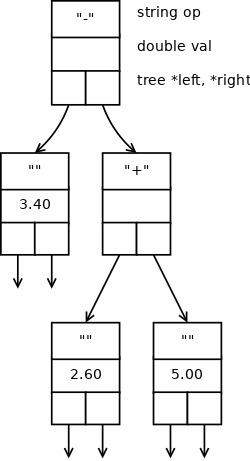
Here is how we build it in code. Note that we have to make a variable for each node, set each variable’s values, then link the variables together.

Tree m;
m.op = "-";
Tree p;
p.op = "+";
Tree v1;
v1.val = 3.4;
Tree v2;
v2.val = 2.6;
Tree v3;
v3.val = 5.0;

m.left = &v1;
m.right = &p;

p.left = &v2;
p.right = &v3;

v1.left = v1.right = v2.left = v2.right = v3.left = v3.right = NULL;

This code makes the variable m (for “minus”) the top node, i.e. the “root” of the tree.

Processing the tree: printing its values

Now, suppose you have a tree; actually, suppose you have a variable root that’s a pointer to a tree. For example,

Tree *root = &m;

Starting with this “root” pointer, how do we get to all the nodes in the tree, and print their values? Specifically, how do we print the values in the tree in such a way as to arrive at an equivalent arithmetic expression (perhaps with extra parentheses)?

Our task is to take the tree we’ve defined and print the contents of the tree in this form: (3.4-(2.6+5.0))

You’ll notice that the printed form of the tree follows a simple pattern: for every operation, print a (, then the contents of the left subtree, then the operation (e.g. +), then the contents of the right subtree, finally a ).

Unlike linked lists, trees are non-linear, so we cannot process them in a linear manner. For some node in the tree, we cannot know how big a subtree there is on the left side or the right side. So we cannot simply set up a loop to process the left and right subtrees; instead, we must resort to a recursive procedure.

Recall, from the Recursion lecture notes, that a recursive procedure (recursive function) refers back to itself. Also, notice that the description above of how to print the contents of the tree was a recursive description: “print a (, then the contents of the left subtree, then …” Suppose we call this process print_tree. Then we can rewrite the description like this:

The print_tree procedure works as follows: Print a (. Then, follow the print_tree procedure (this very same procedure) on the left subtree. Then, print the operation (e.g. +). Then, follow the print_tree procedure on the right subtree. Finally, print a ).

There are a few minor problems with that description. First, if the node is just a value (that is, op == ""), then we just print the value and don’t bother with ( or ) or left and right subtrees (values don’t have left or right subtrees; those pointers are NULL pointers). Also, if there is no tree (the node we’re looking at is just a NULL pointer), then we don’t need to do anything.

Now we can code this procedure in C++, as a function:

void print_tree(Tree *root)
{
    if(root == NULL)
        return;
    
    if(root->op == "")
    {
        cout << root->val;
    }
    else
    {
        cout << "(";
        print_tree(root->left);
        cout << root->op;
        print_tree(root->right);
        cout << ")";
    }
}

Using the function like this: print_tree(root) results in the printout (3.4-(2.6+5)), which is just what we want.

A slight variation: handling other kinds of operators

In Homework 5, you must be able to work with binary and unary operators/functions; that is, your tree nodes may have +, -, etc. operators (binary operators), and log, sin, etc. functions (unary functions). If we use the same print_tree function with a tree that has unary functions in it, we get output that doesn’t look right.

For example, the tree

       /
      / \
     /   \
    /     \
  sin     cos
  /       /
4.00    4.00

…prints as ((4sin)/(4cos)) (do you see why?).

We can fix this by adding another conditional in our code. Homework 5 states that a function like log or sin has only a left subtree, and no right subtree (while operators +, -, etc. always have subtrees on both sides). So, we simply check if we have an operator and there is no right subtree; if so, we print the operator first, then (, then the left subtree, then ).

void print_tree(Tree *root)
{
    if(root == NULL)
        return;
    
    if(root->op == "")
    {
        cout << root->val;
    }
    else if(root->right == NULL)
    {
        cout << root->op;
        cout << "(";
        print_tree(root->left);
        cout << ")";
    }
    else
    {
        cout << "(";
        print_tree(root->left);
        cout << root->op;
        print_tree(root->right);
        cout << ")";
    }
}

Now, that same tree prints as (sin(4)/cos(4)), which is what we want.